Rendering the Mandelbrot Set on the C64
Overview
I recently got a Commodore 64 as a present and, after the obligatory Hello World program, I set my sights on trying to render out an image of the Mandelbrot set. It also seems like a nice familiar yet non-trivial program to get to grips with BASIC with; with a few challenges and a satisfying result.
I won't go into the details of what the Mandelbrot set is, on the assumption that you already know; you likely wouldn't have clicked on this page otherwise!
Development
At first, I sat down in front of my breadbin of a C64 to learn how to even use the thing, and to read up on the basics of BASIC. Something about reading the physical manual held in my physical hand, reading physically printed words which were typeset in the early '80s was really satisfying. Some of the lines and arrows were very obviously hand drawn and I'm sure Letraset was likely used here or there.
Limiting myself to just the one resource in front of me, without googling a whole lot or jumping from site to site every time I needed to learn a new piece of syntax was quite refreshing; it forced me to really read the manual and experience the charm dated simplicity.
After tapping away for a while, I decided to chicken out. I powered it down and jumped onto my Windows 11 PC to start developing the program using a modern IDE (CBM prg Studio) and emulator (VICE), for a couple of reasons:
- A nice modern IDE environment greatly speeds up development with features such as
- a usable amount of screen space,
- automatic renumbering of lines for easier editing,
- and pretty colours.
- An emulator can instantly be launched and can be sped up, which really brings down the time it takes to test my dodgy code and weed out all the bugs.
The C64 happily handles fractional and negative numbers, but it can't handle complex numbers and so the real and imaginary components of the result have to be split and computed separately. Let's say that and :
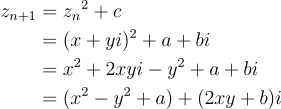
so for each iteration, the real component becomes and the imaginary component becomes .
Before diving into creating any fractals, I first got familiar with the C64's Standard High-Resolution Bit Map Mode allowing for a pixel resolution, with each pixel being directly controllable, and plotted the following sinusoid:
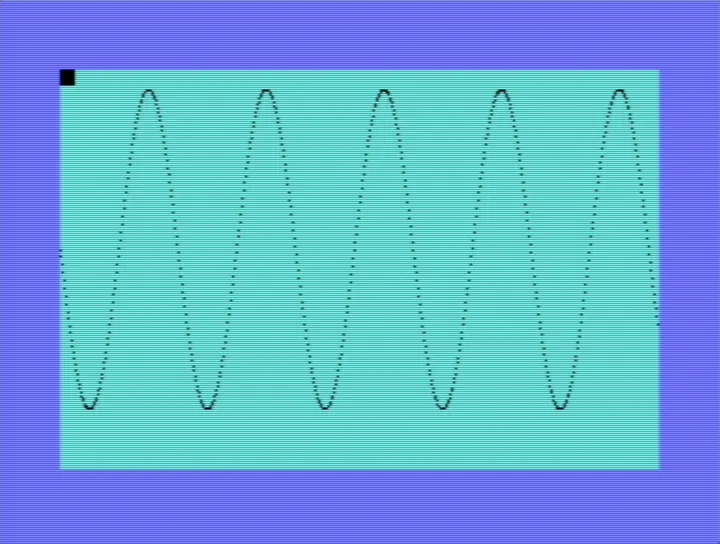
After much pain and gripe (many hours of it), I managed to get some working code on the emulator with an output I was happy with - the end of this page for a verbatim copy.
Running the program
After typing out my code and double checking for any mistakes, I entered RUN and was graced with the following output!


Of course this wasn't instant... With 3 nested loops and some serious number-crunching, this program isn't cheap for hardware of this age. Especially if the poor C64 running it has to deal with some newbie's un-optimised BASIC for hours on end. As such, the above image took approximately 35-40 hours to render! This corroborates this Reddit post by Paul Soper (which was partly the inspiration for this project); their code took 36 hours to run.
Conclusion
This was a fun exercise. It was nice and a little enlightening to use an older machine, it's an honest interaction. The computer is what it is and works how it works and you as the user can do whatever you want with that.
It was also fun to use BASIC and see the parallels to its modern iterations. I find myself writing Inventor scripts in VBA (out of necessity, not choice) at work. Out of curiosity, I tried to use syntactic features that I'd learned on the C64 and had never seen in a VBA environment such as REM and :, and they worked in the same way!
In future, when I muster the motivation, I'd like to alter the program to add colour. I could also dip my toes into learning machine language to write a more performant variant. Until then, I'll definitely be playing around a lot more with this fun little machine.
The code
Below is the full program. Note that the magnitude MG of each iteration value is not square rooted (is that a even valid verb?), to save an operation, since it's being compared to some arbitrary integer stand-in for infinity anyway. Not sure how much time that saved, and I don't have the patience to test it...
10 REM MANDELBROT - BITMAP MODE
20 REM J. PHILBRICK - JUNE 2025
30 BS = 2*4096
40 POKE 53272, PEEK(53272) OR 8 : REM PUT BITMAP AT 8192
50 POKE 53265, PEEK(53265) OR 32 : REM ENTER BIT MAP MODE
60 REM CLEAR BIT MAP AND THEN SET COLOUR
70 FOR I = BS TO (BS + 7999) : POKE I, 0 : NEXT
80 FOR I = 1024 TO 2023 : POKE I, 3 : NEXT
90 POKE 1024, 1
100 MX = 3 : IT = 15 : REM BOUND CEIL & ITER
110 CX = -1 : RX = -1 : REM COL CNT & ROW CNT
120 IU = 1.2 : REM IMAG UPPER
130 IL = -1.2 : REM IMAG LOWER
140 RU = 1.0 : REM REAL UPPER
150 RL = -2.0 : REM REAL LOWER
160 SI = (IU - IL) / 200 : REM IMAG STEP
170 SR = (RU - RL) / 320 : REM REAL STEP
180 FOR R = IL TO IU STEP SI
190 RX = RX + 1 : CX = -1
200 FOR C = RL TO RU STEP SR
210 CX = CX + 1
220 RS(0) = 0 : REM REAL PART RESULT
230 RS(1) = 0 : REM REAL PART RESULT
240 FOR K = 0 TO IT
250 T0 = RS(0)
260 T1 = RS(1)
270 RS(0) = T0^2 - T1^2 + C
280 RS(1) = T0*2 * T1 + R
290 REM ABS MAGNITUDE
300 MG = RS(0)^2 + RS(1)^2
310 IF MG >= MX THEN 420 : END
320 NEXT K
330 REM POKE FILL
340 CH = INT(CX/8)
350 RO = INT(RX/8)
360 LN = RX AND 7
370 BI = 7 - (CX AND 7)
380 BY = BS + RO*320 + CH*8 + LN
390 POKE 1024, 10
400 POKE BY, PEEK(BY)OR(2^BI)
410 GOTO 430
420 POKE 1024, 0
430 NEXT C : NEXT R
440 POKE 1024, 2
450 GOTO 450 : REM INF LOOP TO PAUSE EXECUTION
